Operaciones con matrices

OPERACIONES CON MATRICES

Suma

La suma de dos matrices de orden mxn es otra matriz dimensión mxn.

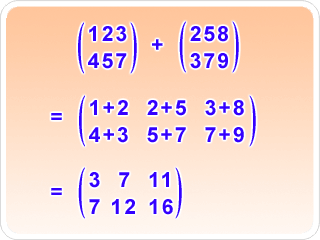
Producto de un numero real por una matriz

Dada una matriz A = (a_ij) y un número real k , se define el producto de un número real por una matriz: a la matriz de la misma dimensión que A, en la que cada elemento está multiplicado por k.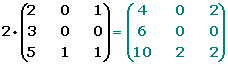

Producto de matrices

Dos matrices A y B se dicen multiplicables si el número de columnas de A coincide con el número de filas de B.

A_{m x n} x B_{n x p} = C_{m x p}

El elemento c_ij de la matriz producto se obtiene multiplicando cada elemento de la fila i de la matriz A por cada elemento de la columna j de la matriz B y sumándolos.

Aquí se anexan unas presentaciones útiles para comprender mejor como se realizan la suma y multiplicación de matrices.

Suma de matrices from Ana Robles

Álgebra Lineal - Multiplicación de Matrices (2x2) from Ricardo Alejos

Tipos de Matrices

TIPOS DE MATRICES

Matriz fila

Una matriz fila está constituida por una sola fila.

Matriz columna

La matriz columna tiene una sola columna

Matriz rectangular

La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn.

Matriz traspuesta

Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.

Matriz nula

En una matriz nula todos los elementos son ceros.

Matriz cuadrada

La matriz cuadrada tiene el mismo número de filas que de columnas.

Los elementos de la forma a_ii constituyen la diagonal principal.

La diagonal secundaria la forman los elementos con i+j = n+1, siendo n el orden de la matriz.

Itroduccion a la Materia

Las matemáticas o la matemática es una ciencia formal que, partiendo de axiomas y siguiendo el razonamiento lógico, estudia las propiedades y relaciones entre entidades abstractas como números, figuras geométricas o símbolos.

Para explicar el mundo natural se usan las matemáticas, tal como lo expresó Eugene Paul Wigner (Premio Nobel de física en 1963):

La enorme utilidad de las matemáticas en las ciencias naturales es algo que roza lo misterioso, y no hay explicación para ello. No es en absoluto natural que existan “leyes de la naturaleza”, y mucho menos que el hombre sea capaz de descubrirlas. El milagro de lo apropiado que resulta el lenguaje de las matemáticas para la formulación de las leyes de la física es un regalo maravilloso que no comprendemos ni nos merecemos.

El álgebra lineal es una rama de las matemáticas que estudia conceptos tales como vectores, matrices, sistemas de ecuaciones lineales y su enfoque de manera más formal, espacios vectoriales y sus transformaciones lineales.

Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas, como el análisis funcional, las ecuaciones diferenciales, la investigación de operaciones, las gráficas por computadora, la ingeniería, etc.

En esta ocasión estaremos estudiando lo relacionado con matrices. 

Generalidades de las Matrices

Matrices.

Definición:

Se denomina matriz a todo conjunto de números o expresiones dispuestos en forma rectangular, formando filas y columnas.

Elemento de una matriz:

Cada uno de los números de que consta la matriz se denomina elemento.

Un elemento se distingue de otro por la posición que ocupa, es decir, la fila y la columna a la que pertenece.

Dimensión de una matriz:

El número de filas y columnas de una matriz se denomina dimensión de una matriz. Así, una matriz de dimensión mxn es una matriz que tiene m filas y n columnas.

De este modo, una matriz puede ser de dimensión: 2x4 (2 filas y 4 columnas), 3x2 (3 filas y 2 columnas), 2x5 (2 filas y 5 columnas), etc.

Sí la matriz tiene el mismo número de filas que de columnas, se dice que es de orden: 2, 3, 4, etc

El conjunto de matrices de m filas y n columnas se denota por  A_mxn o (a_ij).

Un elemento cualquiera de la misma, que se encuentra en la fila i y en la columna j, se denota por a_ij.